Tabla de frecuencias y gráficos estadísticos

Tablas de frecuencias para datos no agrupados

En estadística el proceso de recolección de datos es una de las primeras etapas que se deben de llevar a cabo al momento de realizar un estudio, el cual nos permitirá tener una visión mas clara de la información y por ende se nos hará más fácil el análisis de los resultados y de la redacción de conclusiones.

Para empezar con la distribución de datos cuantitativos tendremos un ejemplo, el cual consiste en la edad de 30 personas (tomadas de forma aleatoria), las cuales asistieron a ver una película en un cine de Managua, Nicaragua.

EDADES

8	11	13	19	30
7	10	12	18	26
7	10	13	18	28
6	10	12	16	25
5	9	11	13	21
5	9	11	15	24

1°) Ordenar los datos de menor a mayor

2°) Identificar el valor menor y el valor mayor

3°)Se recomienda para este ejemplo tomar una amplitud de 5

4°) Agrupar los datos en intervalos, empezando del menor valor, el cual en este caso es el 5 y empezar a contar a partir de ese valor una amplitud de 5

5-6-7-8-9 (de 5 hasta 9); el siguiente intervalo empieza en 10: 10-11-12-13-14 (de 10 hasta 14) y así sucesivamente hasta completar todos los intervalos.

6°) Cuántos intervalos vamos a construir: vamos a detenernos hasta que se llegue al valor mayor de nuestros datos, en este caso en es el 30, por lo tanto el ultimo intervalo tiene que ser mayor o igual a 30.

veamos la agrupación de la tabla de frecuencias

Intervalos	frecuencia	fr	fr%	f.a	AC(°)
5  - 9	8	0.267	26.667	8	96
10  - 14	11	0.367	36.667	19	132
15  - 19	5	0.167	16.667	24	60
20  -  24	2	0.067	6.667	26	24
25  -  29	3	0.100	10.000	29	36
30 - 34	1	0.033	3.333	30	12
Total	30	1	100	--	360

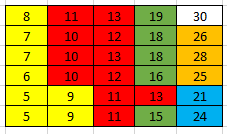
Frecuencia: La frecuencia es el numero de veces que se repite un numero cualquiera, en el caso de la frecuencia de los intervalos se determina contando cuantos datos hay entre 5 y 9 incluyendo dichos valores, lo marcados en amarillo están dentro del intervalo de 5 - 9 son 8 datos, en la clase de 10 - 14 los marcados en rojo son 11 datos y así mismo se hace con el resto de los datos.

La frecuencia absoluta o total, es la suma de todas las frecuencias la cual es 30 y tiene que coincidir con el numero de datos mostrados al inicio del problema planteado.

Frecuencia relativa: es una relación entre cada frecuencia y la frecuencia absoluta, para este caso se obtuvo dividiendo 8/30= 0.267, luego 11/30= 0.367, y así hasta llegar al ultimo valor 1/30= 0.033

la suma de la frecuencia relativa (fr) tiene que ser igual a 1 o aproximarse a la unidad (1), en su defecto tiene que dar una cifra entre 0.9-0.999; esto se debe al error de redondeo en la cantidad obtenida durante la división efectuada para calcular la frecuencia relativa. 

frecuencia relativa porcentual (fr%): se determina multiplicando el valor de la fr por 100.

fr%=fr*100

la suma de la frecuencia relativa porcentual debe ser igual al 100%

frecuencia acumulada (fa): consiste en escribir el primer valor de la frecuencia, en este caso es 8 y posteriormente se le va sumando la frecuencia siguiente (8+11=19), a este valor obtenido se le suma la frecuencia siguiente (19+5=24), y al nuevo valor se le suma la frecuencia siguiente y así sucesivamente hasta llegar a la ultima frecuencia y el valor que se obtiene al final debe ser igual al de la frecuencia absoluta como se puede apreciar en la tabla de distribución de frecuencias ( frecuencia acumulada no se suma al final). 

Ángulo central AC(°): Se calcula con el propósito de construir el diagrama de pastel o de sectores y es la medida de los ángulos que le corresponden a cada intervalo en dependencia del porcentaje de cada uno de ellos, a mayor porcentaje mayor será la porción que se le asignara en el gráfico, esta medida del ángulo central está en grados y se obtiene al multiplicar  la frecuencia relativa por 360°.

AC(°)=fr*360 

GRÁFICOS ESTADÍSTICOS 

Entre los mas comunes tenemos el diagrama de barras, diagrama de pastel o de sectores, histograma con su polígono de frecuencia y el gráfico de ojiva, para este ejemplo se construyeron los tres primeros que se mencionaron.

Gráfico de barras.

Se puede observar que el mayor numero de asistentes rondan entre las edades de 10 a 14 años y le sigue personas entre las edades de 5-9 años.

Gráfico de pastel o de sectores:

De los asistentes el 3% tenían entre 30 a 34 año de edad, los cuales representan la minoría, siendo los que  más asistieron a ver la película personas jóvenes (niños) entre 10 a 14 años con un 36%

Histograma

Puedes descargar la hoja de calculo en excel para efectuar cualquiera de las operaciones descritas en el procedimiento anterior, ademas puedes utilizar dicha hoja para resolver cualquier ejercicio, solo debes de sustituir los datos existentes por los que tu desees. 

accede al siguiente link de descarga, sigue los pasos siguientes:

    

  Para ver el contenido a descargar 

   1)  Deben marcar en no soy un robot

   2)      Luego en click here to continue..

   3)      Debe esperar 12segundos     

   4)      Luego en la parte superior derecho das en SKIP AD

   5)      Ve y descarga el contenido

    http://flyligas.com/N64OTk